Atividade 01 - Shredding a photo

A experiência do vídeo consiste em mostrar como "quadruplicar" a foto de um cachorro colocando a imagem em um cortador de massas e distribuindo as fatias de modo a formar novas imagens.

Primeiro é cortado a foto com o cortador de massas na vertical e reorganizado de modo a duplicar a foto.

Depois de as imagens serem juntadas lado a lado é cortado de novo a foto, porém o corte é feito na horizontal de modo a duplicar novamente cada foto. As duas fotos viram um total de quatro imagens.

O resultado é surpreendente, no qual é possível "transformar" uma imagem em quatro "réplicas" de menor tamanho e qualidade, mas com a mesma proporção da original.
Uma das explicações, além do modelo matemático apresentado logo abaixo, é que a foto foi cortada em pedaços grandes que proporcionam pouca perda de informação. Então ao juntar os pedaços de forma estratégica é possível reproduzir uma nova imagem que tem informação suficiente para identificar que é parecida com a original.

MODELO MATEMÁTICO
A imagem é transformada em uma matriz. O primeiro corte na vertical estabelece as colunas, sendo 22 colunas exatamente. Já o segundo corte na horizontal estabelece as linhas, sendo 16 linhas. Ao total são formados 352 (22 x 16) quadradinhos que formam a imagem como um todo.
Logo, o grande segredo é fazer um rearranjo para "quadruplicar" essa foto. Esse rearranjo é feito sempre dividindo colunas e linhas em pares e ímpares.
Para exemplificar, vamos criar uma matriz de 8x6.

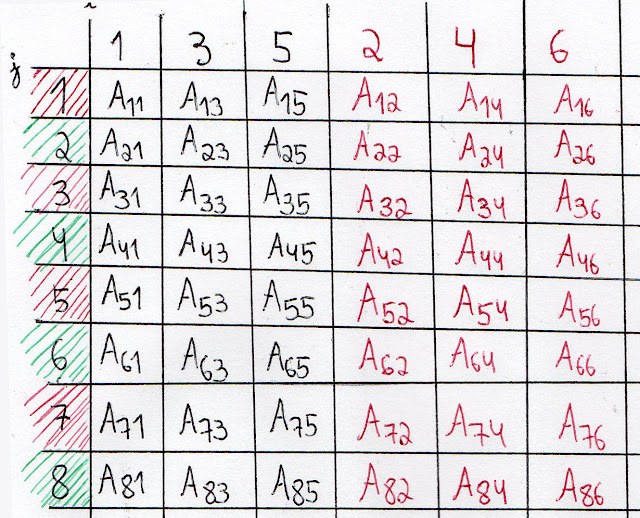
Matriz A

i = linha / j = coluna

A matriz "A" é uma matriz 8x6, onde os elementos são acompanhados por números indicando suas respectivas posições. Há o total de 48 elementos e posições.

Agora é feito o primeiro rearranjo, onde são separadas as colunas pares das ímpares.

Colunas Pares = vermelhos / Colunas Ímpares = azuis

A matriz é reorganizada de modo a criar duas matrizes representadas pelos elementos pretos e vermelhos. Os elementos pretos formam a matriz de coluna ímpar e os vermelhos formam a de coluna par. Observa-se que foi feita a primeira duplicação da foto, já que se têm duas matrizes.

O segundo passo é separar as linhas pares das linhas ímpares. 

Linhas Pares = verdes / Linhas Ímpares = Vermelhas

É feito o segundo rearranjo, porém dessa vez na horizontal. As duas matrizes reorganizadas viram quatro matrizes representadas pelos elementos pretos, vermelhos, azuis e verdes. Os elementos pretos e vermelhos representam as matrizes de linhas ímpares e os elementos azuis e verdes formam as de linhas pares. Logo, as duas matrizes são duplicadas gerando quatro matrizes.

Matrizes de linhas ímpares

Matrizes de linhas pares

Juntando as quatro matrizes observa-se que elas representam as quatro fotos do cachorro no vídeo.

Ao final do modelo matemático podemos reorganizar as quatro matrizes formando uma matriz "B" de 8x6 novamente. 

Matriz B

Conclui-se que tanto a matriz "A" quanto a matriz "B" possuem o mesmo número de elementos, provando então que a experiência do vídeo utiliza o reposicionamento dos elementos da matriz de forma estratégica para criar uma nova matriz que "quadruplica" a foto do cachorro.